Crystal Lattice and Unit cells

You are given marbles of diameter 10 mm. They are to be placed such that their centres are lying in a square bound by four lines each of length 40 mm. The number of marbles per unit area is

The figures given below show the location of atoms in three crystallographic planes in a $\mathrm{FCC}$ lattice.



The planes in the unit cell have been highlighted in the diagram below choose the correct option.

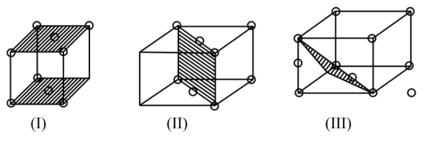
Chromium metal crystallizes with a body centred cubic lattice. The length of the unit cell edge is found to be 287 pm. What would be the density of chromium in $g/c{m}^3$?

The edge length of unit cell of a metal having molecular weight $75g/mol$is $5\AA$ which crystallizes in cubic lattice. If the density is $2g/cc$ then the radius of metal atom $\left(N_A=6\times {10}^{23}\right)$ will be (in pm):

The density of mercury is 13.6 g ml^-1. The approximate diameter of an atom of mercury assuming that each atom is occupying a cube of edge length equal to the diameter of the mercury atom is

The coordination number of a metal crystallizing in a hexagonal close-packed structure is:

Define centred unit cell. What are the types of centred unit cells?

Draw the schematic representation of lattice points in primitive unit cells.

How many types of centred unit cells are there?

_____ unit cells have points at the corners as well as at some other positions.

The correct option for the number of body centred unit cells in all $14$ types of Bravais lattice unit cells is:

The number of lattice points in an end-centred unit cell are:

The co-ordination number of a body-centred atom in cubic structure is:

A substance ${\mathrm{A}}_{\mathrm{x}}{\mathrm{B}}_{\mathrm{y}}$ crystallises in an $\mathrm{f}.\mathrm{c}.\mathrm{c}.$ lattice in which the atoms of $\text{'}\mathrm{A}\text{'}$ occupy each corner of the cube and the atoms of $\text{'}\mathrm{B}\text{'}$ occupy the centres of each face of the cube. Identify the correct composition of the substance ${\mathrm{A}}_{\mathrm{x}}{\mathrm{B}}_{\mathrm{y}}$.

A solid has a structure in which $\mathrm{W}$ atoms are located at the corners of a cubic lattice, $\mathrm{O}$ atom at the center of the edges and $\mathrm{Na}$ atom at centre of the cube. The formula for the compound is

In a $\mathrm{CCP}$ lattice of $\mathrm{X}$ and $\mathrm{Y}$, the $\mathrm{X}$ atoms are present at the corners, while the $\mathrm{Y}$ atoms are at the face centres. Then the formula of the compound if one of the $\mathrm{X}$ atoms from a corner is replaced by $\mathrm{Z}$atoms is (also mono-valent)?

In a face centred lattice of $\mathrm{X}$ and $\mathrm{Y}$, $\mathrm{X}$ atoms are present at the corners, while $\mathrm{Y}$ atoms are at the face centres. Then, the formula of the compound, if one of the $\mathrm{X}$ atoms is missing from a corner in each unit cell, is:

In the cubic structure of a compound which is made from $\mathrm{X}$ and $\mathrm{Y}$, $\mathrm{X}$ atoms are at the corners of the cube and $\mathrm{Y}$ atoms are at the face centres of the cube. The molecular formula of compound is

${\mathrm{MgAl}}_2{\mathrm{O}}_4$ is found in the spinal structure, in which ${\mathrm{O}}^{2-}$ ions constitute the $\mathrm{CCP}$ lattice, ${\mathrm{Mg}}^{2+}$ ions occupy $1/8$th of the tetrahedral voids and ${\mathrm{Al}}^{3+}$ ions occupy $1/2$ of the octahedral voids. Find the total positive charge contained in one unit cell.

In a face centred lattice of $\mathrm{X}$ and $\mathrm{Y}$, $\mathrm{X}$ atoms are present at the corners, while $\mathrm{Y}$ atoms are at the face centres. Then, the formula of the compound is: